Juros Simples

Nos juros simples, a taxa de juros só incide sobre o valor inicial, não considerando o valor acumulado. Por exemplo, se você investiu 1.000 a uma taxa de rendimento de 60% ao ano, após 3 anos teria 2.800:

Nesse exemplo, a cada ano acumularia sempre os mesmos 600 (60% de 1.000), não importando o valor já acumulado no ano anterior (ao contrário dos juros compostos):

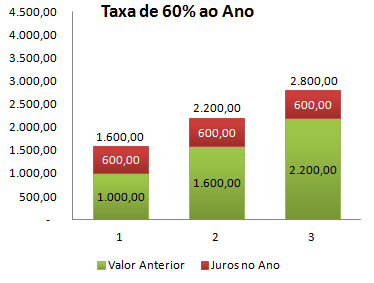
No cálculo acima, o "valor futuro" representa o quanto você teria ao final do período, e os "juros" representa quanto o dinheiro renderia. O mesmo cálculo pode ser utilizado no contexto de um empréstimo, onde o "investimento inicial" seria na verdade o "empréstimo inicial", enquanto o "valor futuro" representaria o valor devido após o período (em meses ou anos).

Fórmulas dos Juros Simples

Fórmula do Valor Futuro (ou Montante):

F = P.(1 + i.n)

Fórmula dos Juros:

J = P.i.n

Onde:

F = valor futuro (muitas vezes chamado de M ou "montante")
J = juros
P = valor presente (muitas vezes chamado de "principal")
i = taxa de juros (normalmente na forma percentual)
n = número de períodos (em dias, meses, anos, ... dependendo do contexto)

Demonstração / Dedução:

F₁ = P + P.i (é o valor futuro após 1 mês)
F₂ = P + P.i + P.i (é o valor futuro após 2 meses)

Repetindo para n meses, pode ser escrita como:

F = P + P.i.n (é o valor futuro após n meses)

Ou colocando o termo P em evidência:

F = P.(1 + i.n)

Observe que o termo P.i.n corresponde aos juros, portanto:

J = P.i.n

Calculadora Online de Juros Simples

Podemos utilizar variações da fórmula do valor futuro, para descobrir qualquer uma das 4 variáveis a partir dos valores das outras 3:

De maneira similar, podemos utilizar as variações da fórmula dos Juros:

Observe que as variações acima são obtidas a partir de simples manipulações algébricas, de forma a "isolar" a variável de interesse. Como regra geral, qualquer problema de juros simples pode ser resolvido analisando qual dessas variações será utilizada, vide exemplos a seguir.

Exemplos

1. Qual a taxa de juros simples para que 1.000 se torne 1.200 em 6 meses?

Utilizando a variação 3 da calculadora online ( i = (F - P)/(P.n) ), teremos:

valor presente: 1.000; valor futuro: 1.200; número de períodos: 6
Solução: i = (1200 - 1000)/(1000*6) = 3,33%

2. Qual os juros simples de 1.000 a taxa de 10% a.t. por 2 meses e 10 dias?

Primeiro devemos converter o período em dias e os juros para "ao dia":

2 meses e 10 dias = 70 dias (assumindo 1 mes = 30 dias)
10% a.t. -> 10%/90 = 0,1111% a.d. (a.t. significa "ao trimestre" e a.d. "ao dia")

Agora utilizando a variação 5 da calculadora online ( J = P.i.n ), teremos:

valor presente: 1.000; taxa de juros: 0,1111%; número de períodos: 70
Solução: J = 1000*0,1111%*70 = 77,77

Observe que 0,1111% é o mesmo que 0,1111/100 e isso vale para qualquer valor percentual.

3. Qual os juros simples produzidos por 5.300, aplicados à taxa de 24% a.a., durante 7 meses?

Primeiro devemos converter os juros para "ao mês":

24% a.a. -> 24%/12 = 2% a.m. (a.a. significa "ao ano" e a.m. "ao mês")

Agora utilizando a variação 5 da calculadora online ( J = P.i.n ), teremos:

valor presente: 5.300; taxa de juros: 2%; número de períodos: 7
Solução: J = 5.300*2%*7 = 742,00

4. Qual o valor que aplicado a juros simples de 0,9% a.m. renderia 1.300 de juros em 105 dias?

Primeiro devemos converter o período em meses:

105 dias = 105/30 = 3,5 meses (assumindo 1 mes = 30 dias)

Agora utilizando a variação 6 da calculadora online ( P = J/(i.n) ), teremos:

juros: 1.300; taxa de juros: 0,9%; número de períodos: 3,5
Solução: P = 1.300/(0,9%*3,5) = 41.269,84

5. Para uma taxa de rendimento de 75% ao ano, em quantos meses um valor irá dobrar através de capitalização simples?

Primeiro devemos converter os juros para "ao mês":

75% a.a -> 75%/12 = 6,25% a.m (a.a. significa "ao ano" e a.m. "ao mês")

Agora utilizando a variação 4 da calculadora online ( n = (F - P)/(P.i) ), teremos:

valor presente: 1; valor futuro: 2; taxa de juros: 6,25%
Solução: n = (2 - 1)/(1*6,25%) = 16

O truque acima consiste na utilização de valores fictícios para F e P de forma a atender ao enunciado do problema, ou seja, usar um valor para F que seja o dobro de P, como por exemplo P=1 e F=2. O problema tambem pode ser resolvido por manipulação algébrica, considerando que F=2*P:

n = (F - P)/(P*i) -> n = (2*P - P)/(P*i) -> n = P/(P*i) -> n = 1/i = 1/6,25% = 16

Home | Topo | Sobre | Fale Conosco

O fazAconta têm fins didáticos e seus exemplos buscam a simplicidade para facilitar a leitura e a compreensão. Todo o conteúdo é constantemente revisado, mas não há qualquer garantia da completa precisão e acerto. Ao utilizar o fazAconta, você concorda que leu e aceitou nossos termos de uso.
Copyright 2008-2020 by BTonetto Creations - Todos os Direitos Reservados.

Resultados Instantâneos

Juros Simples

Fórmulas dos Juros Simples

Calculadora Online de Juros Simples

1. Valor Futuro (ou Montante): `F = P.(1 + i.n)`

2. Valor Presente (ou Principal): `P = F/(1 + i.n)`

3. Taxa de Juros: `i = (F - P)/(P.n)`

4. Número de Períodos: `n = (F - P)/(P.i)`

5. Juros: `J = P.i.n`

6. Valor Presente (ou Principal): `P = J/(i.n)`

7. Taxa de Juros: `i = J/(P.n)`

8. Número de Períodos: `n = J/(P.i)`

Exemplos

Resultados Instantâneos

Juros Simples

Fórmulas dos Juros Simples

Calculadora Online de Juros Simples

1. Valor Futuro (ou Montante): F = P.(1 + i.n)

2. Valor Presente (ou Principal): P = F/(1 + i.n)

3. Taxa de Juros: i = (F - P)/(P.n)

4. Número de Períodos: n = (F - P)/(P.i)

5. Juros: J = P.i.n

6. Valor Presente (ou Principal): P = J/(i.n)

7. Taxa de Juros: i = J/(P.n)

8. Número de Períodos: n = J/(P.i)

Exemplos

1. Valor Futuro (ou Montante): `F = P.(1 + i.n)`

2. Valor Presente (ou Principal): `P = F/(1 + i.n)`

3. Taxa de Juros: `i = (F - P)/(P.n)`

4. Número de Períodos: `n = (F - P)/(P.i)`

5. Juros: `J = P.i.n`

6. Valor Presente (ou Principal): `P = J/(i.n)`

7. Taxa de Juros: `i = J/(P.n)`

8. Número de Períodos: `n = J/(P.i)`