Resultados Instantâneos
Altere qualquer valor acima e o fazAconta mostra instantaneamente os resultados!
Valor Presente
O estudo do Valor Presente ou Valor Atual (siglas VP, VA ou PV) permite comparar valores futuros com um valor no presente, levando em consideração uma taxa de juros para a correção do dinheiro no tempo. Em outras palavras, dado uma série de valores futuros é possível calcular o valor presente equivalente.
Fórmula do Valor Presente
A fórmula P = F/(1 + i)n dos juros compostos precisa ser estendida para contemplar mensalidades:
Onde:
P = valor presente (também chamado VA ou PV)
M = mensalidade (ou outro pagamento periódico, também chamado PGTO ou PMT)
n = número de períodos (em dias, meses, anos, ..., também chamado NPER)
i = taxa de juros (normalmente na forma percentual, também chamado TAXA ou RATE)
Demonstração / Dedução:
=> P.(1+i)n = F - M.[(1+i)n - 1]/[(1+i) - 1] =>
=> P = F/(1+i)n - M.[(1+i)n - 1]/{(1+i)n.[(1+i) - 1]} =>
=> P = F/(1+i)n - M.[(1+i)n - 1]/[(1+i)n+1 - (1+i)n]
Vale observar que P é função inversa de F e vice-versa, por isso, uma pode ser obtida a partir da manipulação algébrica da outra.
Por outro lado, o Excel e outras planilhas eletrônicas oferecem a função VA (ou PV no Excel em inglês) que implementa a fórmula acima e simplifica a vida do usuário:
Observe que o sinal de menos no M e no F trata-se de uma convenção do Excel e é necessário atentar para ela. Veja abaixo exatamente como utilizar essa função (vide ícone  ).
).
Parcelamentos
Suponha que você queira comprar uma TV que custe 2.000,00 e tenha as opções de pagar à vista ou parcelar em 20x de 110,00. Qual a melhor opção?
A primeira vista, parcelado sairia por 2.200 e portanto parece melhor comprar à vista. No entanto, devemos considerar que se comprarmos parcelado, poderíamos investir o dinheiro que usaríamos à vista, e dependendo do rendimento, o parcelamento poderia ser a melhor escolha.
Então suponha que você consiga um rendimento de 1,5% ao mês. O cáculo do Valor Presente nos mostra quanto equivaleria a um pagamento à vista. Para isso basta usar a fórmula VA do Excel:
Portanto, neste exemplo só valeria comprar à vista por menos de 1.888,55. Podemos ainda concluir que se você aplicar os 2.000,00 com rendimento de 1,5% e ir retirando cada parcela, no final ainda sobraria 111,45 (que é a diferença 2.000,00-1.888,55).
Diferentes Parcelas
Suponha agora que você tenha as opções de pagar à vista 2000,00 ou parcelar em 3 meses com 3 cheques pré-datados de valores diferentes: 800 / 600 / 650. Para saber a melhor opção basta utilizar a fórmula VAL do Excel:
Ou seja, com os cheques pré-datados você teria uma pequena vantagem de 7,82 com relação ao pagamento à vista.
Saldo Devedor
Se você tem um financiamento e deseja antecipar o pagamento das parcelas restantes, como calcular o saldo devedor? Vale ressaltar que não basta somar as parcelas restantes e o saldo devedor tem que ser menor que essa soma, pois se você esta antecipando o pagamento, não deveria pagar os juros sobre as parcelas com vencimento em uma data futura. O cálculo correto é realizado trazendo as parcelas futuras ao valor presente, conforme detalhado na seção Saldo Devedor.
Equivalência entre VA e VAL
Para parcelas iguais, as duas fórmulas VA e VAL retornam resultados equivalentes. Por exemplo, para ter um resultado equivalente ao VA(1,5%;20;-110), vamos utilizar a VAL passando o 110 vinte vezes:
Conforme esperado, encontramos o mesmo resultado de VA(1,5%;20;-110) = 1.888,55 do primeiro exemplo. Veja ainda a seção Valor Presente Líquido
Valor Presente ou Valor Atual
O Valor Presente também é chamado de Valor Atual, por isso a fórmula no Excel em português se chama VA. Pela mesma razão, a fórmula VAL corresponde ao Valor Presente Líquido ou Valor Atual Líquido.
Análise Gráfica
Vamos aplicar a fórmula VA com diferentes rendimentos para o caso do primeiro exemplo:
VA(0,5%;20;-110) = 2.088,62
VA(1,0%;20;-110) = 1.985,01
VA(1,5%;20;-110) = 1.888,55
VA(2,0%;20;-110) = 1.798,66
Vemos que para uma taxa de juros de 0%, o valor presente seria 2.200 que é soma das parcelas. Vemos ainda que para um rendimento de 0,5% é preferível comprar à vista pois o Valor Presente é maior que o valor à vista (2.088,62 > 2.000,00). Veja o gráfico:
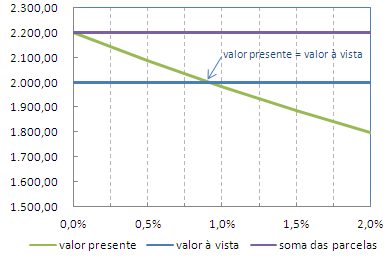
O gráfico mostra que para um rendimento de aproxidamente 0,9% ao mês, o valor presente é igual ao valor à vista, significando que as duas opções de pagamento são igualmente vantajosas.
Conclusões
Para compararmos corretamente um valor à vista com um valor parcelado, devemos calcular o Valor Presente. Se simplesmente compararmos com a soma das parcelas, estamos supondo que somos incapazes de fazer o dinheiro render.
Quando temos um parcelamento sem juros (soma das parcelas igual ao valor à vista), sempre é mais interessante parcelar e aplicar o dinheiro que seria entregue à vista.
Dúvidas Comuns
1. As fórmulas VA e VAL não funcionam no meu Excel ou no Google Spreadsheets. O que há de errado?
Resposta: Se o seu Excel estiver em inglês ou utilizar o Google Spreadsheets, essas fórmulas são denominadas: PV e NPV. Veja a relação completa das fórmulas em portugues e inglês.
Copyright 2008-2020 by BTonetto Creations - Todos os Direitos Reservados.