Resultados Instantâneos
Altere qualquer valor acima e o fazAconta mostra instantaneamente os resultados!
VPL e TIR
O Valor Presente Líquido e a Taxa Interna de Retorno permitem analisar a viabilidade financeira de projetos ou novos negócios, a partir das estimativas dos investimentos iniciais e retornos futuros (fluxos de caixa). Outras denominações:
- Valor Presente Líquido também é conhecido como Valor Atual Líquido, siglas VPL, VAL ou NPV (Net Present Value)
- Taxa Interna de Retorno também é conhecida pelas siglas TIR ou IRR (Internal Rate of Return)
Definição do VPL
Quanto maior o VPL, mais lucrativo será o projeto ou novo negócio. O VPL indica qual o lucro em R$ (ou dólares, ...) que o projeto ou novo negócio trará.
Entenda a seguir porque não basta somar os retornos e subtrair os investimentos, para saber qual o lucro que um projeto ou novo negócio trará.
Fluxo de Caixa Descontado
Um fluxo de caixa representa os investimentos e retornos previstos em um projeto ou novo negócio. Os valores iniciais negativos correspondem ao período em que os investimentos são maiores que os retornos. Suponha que você tenha estimado o seguinte fluxo de caixa para um novo negócio:
| Ano 0 | Ano 1 | Ano 2 | Ano 3 | Ano 4 | |
|---|---|---|---|---|---|
| Fluxo de Caixa | -100 | -100 | 100 | 100 | 100 |
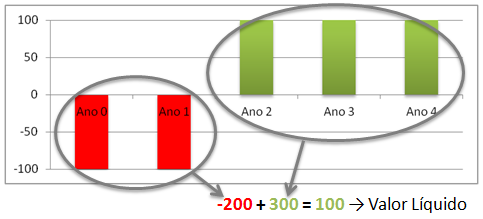
Nesse exemplo, o somatório dos termos (ou Valor Líquido) é 100, ou seja, a soma dos retornos é maior que a soma dos investimentos e o fluxo de caixa parece vantajoso. Entretanto, pelo princípio do valor do dinheiro no tempo sabemos que 100 reais no futuro vale menos do que 100 hoje, mas vale exatamente quanto? Para responder a essa pergunta, basta trazer cada termo à valor presente, utilizando a fórmula P = F/(1 + i)n dos juros compostos:
| Ano 0 | Ano 1 | Ano 2 | Ano 3 | Ano 4 | |
|---|---|---|---|---|---|
| Fluxo de Caixa Descontado* | -100 | -83 | 69 | 58 | 48 |
* Taxa de juros de 20% ao ano
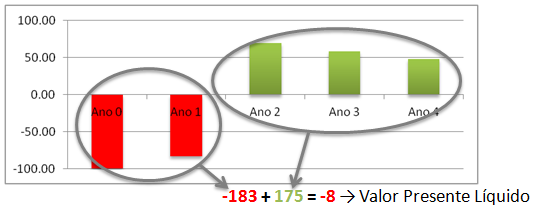
Este é conhecido como Fluxo de Caixa Descontado e a soma dos termos é nada mais, nada menos, que o Valor Presente Líquido (ou VPL). Vemos agora que esse fluxo de caixa não é vantajoso pois o VPL é negativo em -8. No primeiro gráfico vemos que todas as barras tem o mesmo tamanho, enquanto neste gráfico, as 2 barras representando os investimentos acabam sendo maiores que as 3 barras representando os retornos.
Custo de Capital
A taxa de juros acima, também é chamada de custo de capital, e pode ser interpretada de duas formas:
- Taxa de juros na qual você conseguiria captar recursos para financiar o projeto ou novo negócio.
- Taxa de rendimento em um investimento de baixo risco, no qual você poderia aplicar o dinheiro ao invés de investir no projeto.
Cálculo Online do VPL
O fazAconta permite você calcular online o VPL dos seus fluxos de caixa e ainda mostra com utilizar a fórmula VAL do Excel para fazer este mesmo cálculo:
Experimente alterar a taxa de juros para 0% e observe que o resultado equivale a soma dos termos (ou Valor Líquido).
Perpetuidade
Alguns projetos continuarão a gerar retorno por tempo/prazo indeterminado. Experimente acrescentar reticências (...) ao final do fluxo de caixa no Cálculo Online acima e verifique o que acontece.
Definição da TIR
Quanto maior a TIR, melhor e mais lucrativo será o projeto ou novo negócio. Pense na TIR como a taxa de juros que uma aplicação financeira precisaria render para ser tão lucrativa quanto o projeto ou novo negócio.
Cálculo Online do TIR
O fazAconta permite você calcular online o TIR dos seus fluxos de caixa e ainda mostra com utilizar a fórmula TIR do Excel para fazer este mesmo cálculo:
Experimente acima no Cálculo Online do VPL, colocar uma taxa de juros de 17,872% e verifique o que acontece.
Relação entre as Funções VAL e VA
As funções do Excel para o Valor Presente Líquido e Valor Presente podem fornecer resultados iguais:
VA(20%;3;-100) = 210,65
Observe que na função VAL você informa cada termo a ser trazido à valor presente, enquanto na VA você fornece apenas um termo que seria repetido N vezes. Mais detalhes na seção valor presente.
Relação entre o Payback, ROI, VPL e TIR
Além do VPL e TIR, devemos considerar outros 2 cálculos importantes na comparação do retorno financeiro de projetos:
- Tempo de Payback - é tempo para que um projeto se pague, ou seja, a partir do qual o VPL fica positivo.
- Retorno sobre Investimento (ROI) - indica o percentual de retorno sobre o investimento realizado e utiliza o VPL em seu cálculo.
Copyright 2008-2020 by BTonetto Creations - Todos os Direitos Reservados.