Juros Compostos

Nos juros compostos, a cada período é acrescido um valor de juros proporcional ao valor já acumulado, ou seja, a taxa de juros incide sobre o valor acumulado, que aumenta a cada período. Dessa forma, o valor dos juros acrescidos a cada período é sempre crescente.

Por exemplo, se você investiu 1.000 a uma taxa de rendimento de 60% ao ano, após 3 anos teria 4.096:

investimento inicial: taxa de juros: anos:

EMPTY_VAL

EMPTY_EXPRESSION

---

EMPTY_VAL

EMPTY_EXPRESSION

---

  Altere com seus valores!  

Nesse exemplo, no 1º ano acumularia 600 (60% de 1.000), no 2º ano acumularia mais 960 (60% de 1.600) e no 3º ano acumularia mais 1.536 (60% de 2.560), totalizando 3.096 de juros:

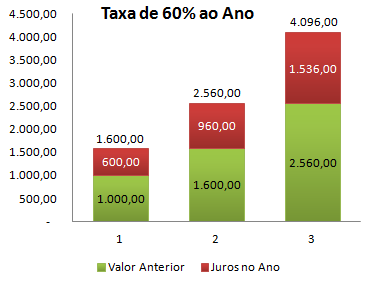
No cálculo acima, o "valor futuro" representa o quanto você teria ao final do período, e os "juros" representa quanto o dinheiro renderia. O mesmo cálculo pode ser utilizado no contexto de um empréstimo, onde o "investimento inicial" seria na verdade o "empréstimo inicial", enquanto o "valor futuro" representaria o valor devido após o período (em meses ou anos).

Fórmulas dos Juros Compostos

Calculadora Online de Juros Compostos

Podemos utilizar variações da fórmula do valor futuro, para descobrir qualquer uma das 4 variáveis a partir dos valores das outras 3:

1. Valor Futuro (ou Montante): F = P.(1 + i)n

---

valor presente: taxa de juros: número de períodos:

EMPTY_VAL

EMPTY_EXPRESSION

2. Valor Presente (ou Principal): P = F/(1 + i)n

---

valor futuro: taxa de juros: número de períodos:

EMPTY_VAL

EMPTY_EXPRESSION

3. Taxa de Juros: i = (F/P)1/n - 1

---

valor presente: valor futuro: número de períodos:

EMPTY_VAL

EMPTY_EXPRESSION

4. Número de Períodos: n = log(F/P)/log(1+i)

---

valor presente: valor futuro: taxa de juros:

EMPTY_VAL

EMPTY_EXPRESSION

---

  Altere com seus valores!  

Observe que as variações acima são obtidas a partir de simples manipulações algébricas, de forma a "isolar" a variável de interesse. Como regra geral, qualquer problema de juros compostos pode ser resolvido analisando qual dessas variações será utilizada, vide exemplos a seguir.

Conversão de Taxa de Juros entre diferentes períodos

No regime de juros simples, uma taxa de juros de 1% a.m. (ao mês), corresponde a uma taxa de 12% a.a. (ao ano), entretanto, no regime de juros compostos, o cálculo é um pouco mais complexo:

Conversor de Taxa de Juros

---

taxa de juros: de:ao diaà semanaao mêsao bimestreao trimestreao semestreao ano para:ao diaà semanaao mêsao bimestreao trimestreao semestreao ano

EMPTY_VAL

EMPTY_EXPRESSION

---

  Altere com seus valores!  

Experimente acima alterar a taxa de juros para 10% e observe que o resultado se afasta muito dos 120% esperados para o regime de juros simples. Veja mais na seção sobre taxa nominal, efetiva e equivalentes.

Exemplos

1. Qual a taxa de juros mensal para que 1.000 se torne 1.200 em 6 meses?

2. Qual o montante de 1.000 a taxa de 10% a.t. por 2 meses e 10 dias?

3. Qual os juros compostos produzidos por 5.300, aplicados à taxa de 24% a.a., durante 7 meses?

Juros Compostos em Mensalidades

Na prática, quando lidamos com empréstimos, parcelamentos ou investimentos, caímos em problemas um pouco mais complexos. Nesses casos precisamos lidar com mensalidades ou anualidades, por exemplo:

• Em um plano de previdência privada, quanto acumularemos se depositarmos mensalmente 400 durante 30 anos, com rendimento mensal de 0,9%? Veja a seção Valor Futuro.


• Quanto pagaremos mensalmente para comprar um carro de 30.000 financiado em 60x iguais a uma taxa de juros de 1,2% ao mês? E se soubermos a mensalidade, mas quisermos verificar a taxa de juros praticada? Veja a seção Tabela Price.


• Quanto devo pagar para quitar as 20 parcelas restantes de uma dívida de 10.000 financiada em 36x a uma taxa de 3,2% ao mês? Veja a seção Saldo Devedor.

Juros Compostos são Injustos?

Já houve muita polêmica sobre os juros compostos, considerando injusto o cálculo de juros sobre juros. Entretanto, os juros compostos são aplicados tanto para dívidas, quanto para investimentos, ou seja, os bancos utilizam a mesma matemática tanto na cobrança de dívidas, quanto na remuneração de investimentos (poupança, CDB, LCI, ...). Então como um Banco ganha dinheiro? A resposta é simples: a taxa de juros paga pelo Banco (quando você deposita ou investe) é sempre menor que a taxa de juros cobrada (quando você pega um empréstimo ou financiamento).

Portanto, os juros compostos são a forma matematicamente correta e justa de aplicar juros ao dinheiro, entretanto alguns bancos cobram juros muito altos ao emprestar dinheiro. Podemos protestar contra os juros abusivos, mas jamais contra a matemática dos juros compostos. Veja o manifesto em defesa dos juros compostos.